The coarsest way to, ahem, classify supervised machine learning (ML) tasks is into classification versus prediction. (What’s supervised ML? See the video below if you need a refresher.)


Let’s start by making sure we’re all on the same page with the basic basics.

Basics: Algorithm vs Model

If you’re new to these terms, I recommend reading this. For the too-busy folk among you, here comes the briefest of reminders:

The point of ML/AI is to automate tasks by turning data (examples) into models (recipes). What do we call the thing that turns examples into recipes? An algorithm.

Now we’re ready to dive in!

What’s the difference between classification, regression, and prediction?

You know those topics that are brainless yet confusing? I hate those topics. This is one of them.

The terminology is daft. On behalf of data science, let me say, “It’s not you, it’s me.” If you’re the kind of person who likes to keep a tidy mind, here’s why your lip might curl in disgust when confronted with the title question:

There is no classification… and regression is something else entirely. Meme template from The Matrix.


There is no classification. The distinctions are there to amuse/torture machine learning beginners. If you’re curious to know what I mean by this, head over to my explanation here. But if you have no time for nuance, here’s what you need to know: classification is what we call it when your desired output is categorical.

Classification is what we call it when your desired output is categorical.

(Need a refresher on categorical data versus other data types? I’ve got you.)

Classification

If you’re looking to automate a classification task, your algorithm’s job is to create a recipe that separates the data, like so:

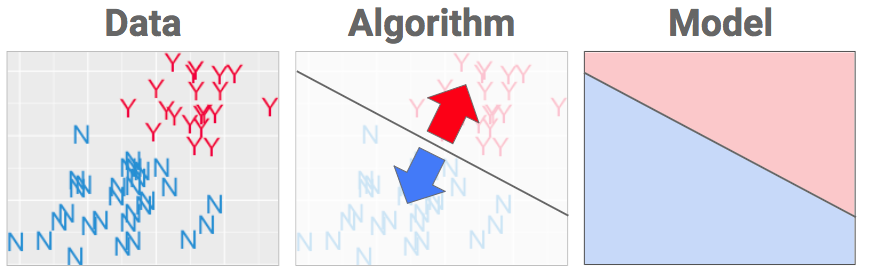
For an example of a classification task plus an overview of algorithms and optimization, see the article where I first used this graphic. The story there was all about separating the good (Yes) bottles of wine from the not-so-yummy (N) bottles.


What we have here is a dataset that is labeled with two classes (Y and N). In other words, the algorithm must put a fence in the data to best separate the Ys from the Ns. Our goal is to create a model that can be used to classify new examples correctly:

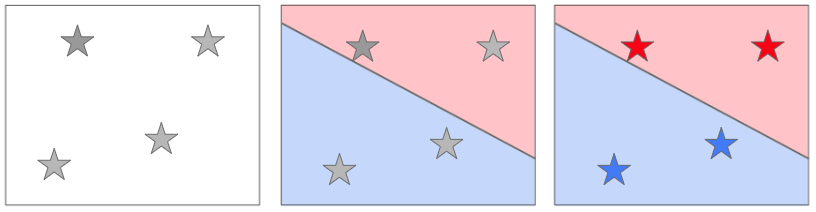
When I get four new bottles of wine, I simply use their input data to figure out where they go on this map, then match them against the recipe’s red and blue regions to label them accordingly.


The algorithm defines WHAT shape will get fitted to the data. The data is used to choose WHERE the best place for that fence is. (“The best” is another way of saying that our answer comes by doing optimization: math that’s all about finding extremes… like the extremely most awesomely bestest place to shove a wall. Learn more here.)

Prediction

If classification is about separating data into classes, prediction is about fitting a shape that gets as close to the data as possible.

If classification is about separating data into classes, prediction is about fitting a shape that gets as close to the data as possible.

The object we’re fitting is more of a skeleton that goes through one body of data instead of a fence that goes between separate bodies of data.

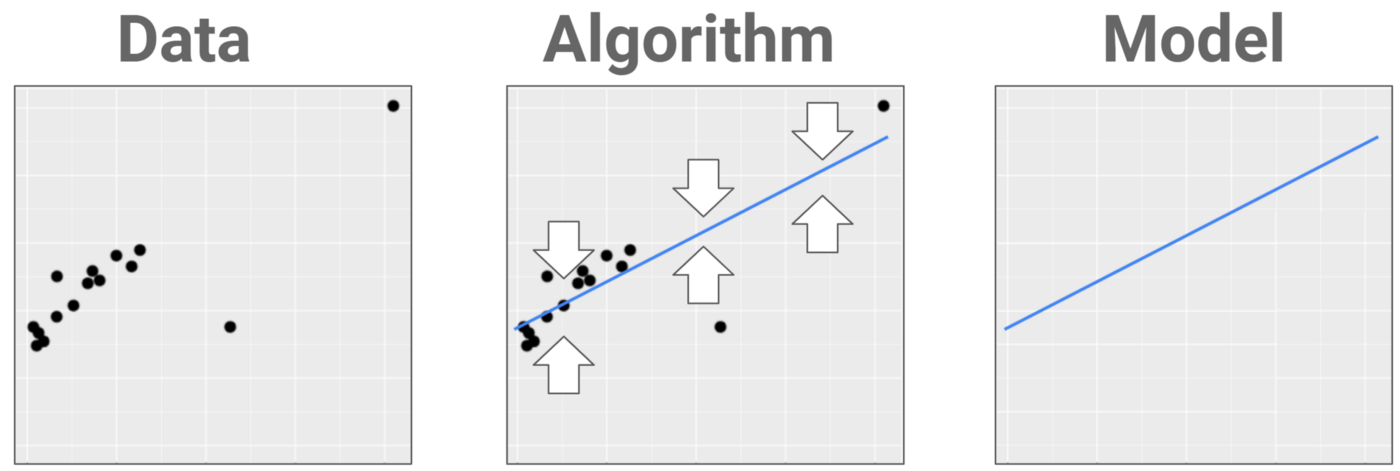
For an example of a prediction task, see my video about linear regression. The story there was all about using data about smoothies to predict their calories. The trickiest thing with understanding what you’re looking at is that the label is contained in the vertical axis of prediction illustrations but in the color/shape of the label in classification illustrations. So the input data is one-dimensional here and two-dimensional in the example above. For the curious, the video does show you what two-dimensional prediction inputs look like.


As before, the algorithm gives you the WHAT and the data gives you the WHERE. When new datapoints come in, they’re plugged into the recipe and the predicted value is read off the line. Want to know more about how that works? Dive into my video on linear regression.

Regression

Some people like to use the term regression task instead of prediction task, which is an unfortunate choice of jargon for at least two reasons:

  1. It’s (yet another) term pilfered by the young field of machine learning from an adjacent older discipline (statistics), apparently without looking up the original meaning. Which would be less impolite if ML/AI didn’t have the audacity to *also* use the original term, which brings me to...
  2. It creates confusion, since the term “regression” is still used in ML/AI the way centuries of statisticians have used it: to refer to a class of algorithms (not tasks). As a result, we get sentences like “our team used logistic regression to perform classification.” *heads explode*

So while “regression” is often used as a synonym for “prediction” in this context, maybe it’s best if we forget I mentioned it at all. (Pinching my nose and moving along quickly.)

Predi-cation?!

Er, that’s not a thing in ML/AI. Just felt you should know that the boundaries get blurry in practice.

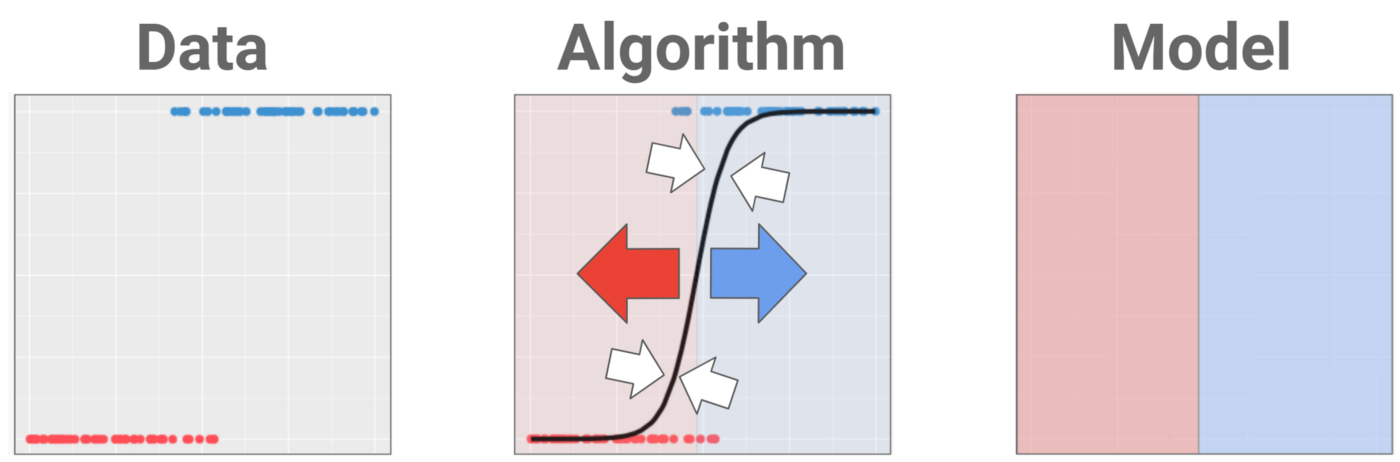
Logistic regression first fits a curve through the data (the categories are coded as 0 and 1 on the y-axis) and then essentially uses the spot where the curve crosses 0.5 on the y-axis to draw the wall for classifying future datapoints. Nuance: in practice, ML engineers keep the original predictive curve (which outputs a probability prediction) since we can always turn the probability prediction into a 0/1 label by rounding the answer off. Why bother at all? Probabilities allow you to do ranking, while the final binary model does not. Additionally, they give you a principled way to nope out of classifying murky cases with probabilities too close to 50%.


For example, you can use a regression algorithm to fit a backbone to your data and then use this backbone to pinpoint the best spot to put a wall, achieving classification with prediction and confusing all the beginners. Which is why I’m always torn about whether to teach this terminology in the first place. But hey, you’ll probably encounter it at some point on your journey, so we may as well cover it.


In my opinion, the classification versus prediction taxonomy is worth knowing in a broad-strokes way — useful to get you started, but not a law of the universe. I mean this in the sense that a professor shouldn’t put “Is this prediction or classification?” questions on an exam because it’ll inspire enterprising students to discover their inner lawyer. They might argue that everything is prediction if you look at it the right way… and they’d be correct.

Original article can be found here