While working on a classification problem, a regression analysis, or another data science project, bagging, and boosting algorithms can play a vital role.
This article summarizes:
#1 the idea of ensemble learning, introduces,
#2 bagging and,
#3 boosting, before a comparison is made between both methods to highlight similarities and differences.
#1: Introduction and idea behind ensemble learning
When we see overfitting or underfitting of our models, it’s necessary to know the key concepts of bagging and boosting, which both belong to the family of ensemble learning techniques:
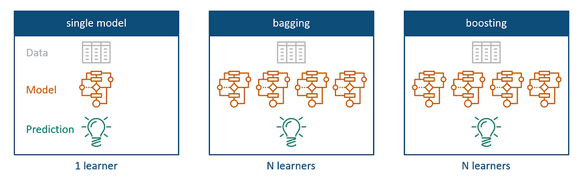
The idea behind ensemble learning comes from the fact that it is the usage of multiple algorithms and models that are used together for the same task. While single models use only one algorithm for predictive analytics, bagging and boosting methods aim to combine several of those to achieve better prediction with higher consistency.
Example: Image classification
Suppose a collection of images, each accompanied by a categorical label corresponding to the kind of animal or creature, is available for the purpose of training a model.
In a traditional modeling approach, several techniques would be tried, and the accuracy of choosing one over the other calculated. Imagine if we used logistic regression, decision tree, and support vector machines here that perform differently on the given data set.
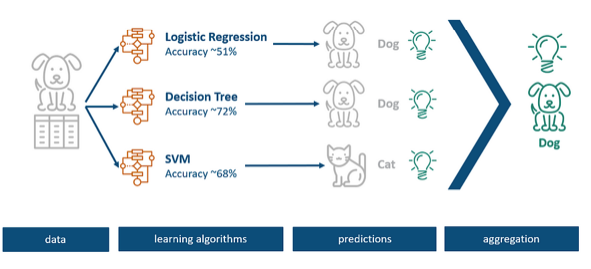
In the above example, it was observed that a specific record was predicted as a dog by the logistic regression and decision tree models, while a support vector machine identified it as a cat. As various models have their distinct advantages and disadvantages for records, it is the key idea of ensemble learning to combine all three models instead of selecting only one approach that shows the highest accuracy.
The above procedure is termed aggregation or voting and combines the predictions of all underlying models, to come up with one prediction that is assumed to be more precise than any sub-model that would stay alone.
Bias-Variance tradeoff
The next chart represents the relationship and the tradeoff between bias and variance on the test error rate. It effectively illustrates the correlation and compromise between bias and variance with respect to the testing error rate.
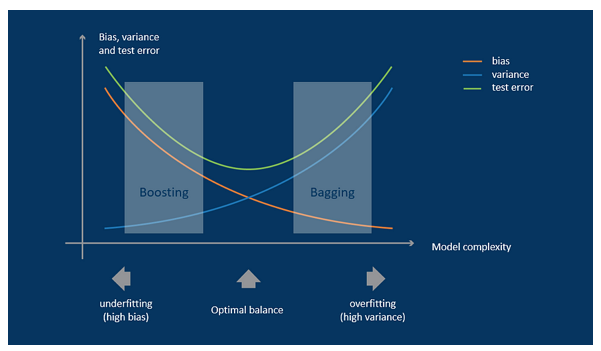
The relationship between the variance and bias of a model is such that a reduction in variance results in an increase in bias, and vice versa. To achieve optimal performance, the model must be positioned at an equilibrium or balancing point, where the error rate is minimized, and the variance and bias are appropriately balanced.
Ensemble learning can help to balance both extreme cases to a more stable prediction. One method is called bagging and the other is called boosting.
#2: Bagging (bootstrap aggregation)
Let’s view the Bagging technique termed bootstrap aggregation. Bootstrap aggregation aims to solve the right extreme of the previous chart by reducing the variance of the model to avoid overfitting.
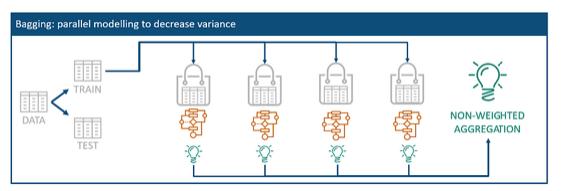
With this purpose, the idea is to have multiple models of the same learning algorithm that are trained by random subsets of the original training data. Those random subsets are called bags and can contain any combination of data. Each of those datasets is then used to fit an individual model which produces individual predictions for the given data. Those predictions are then aggregated into one final classifier.
The calculation of the final ensemble aggregation uses either the simple average for regression problems or a simple majority vote for classification problems. For that, each model from each random sample produces a prediction for that given subset. For the average, those predictions are just summed up and divided by the number of created bags.
#3: Boosting
Boosting is a little variation of the bagging algorithm and uses sequential processing instead of parallel calculations. While bagging aims to reduce the variance of the model, the boosting method aims to reduce the bias to avoid underfitting the data.
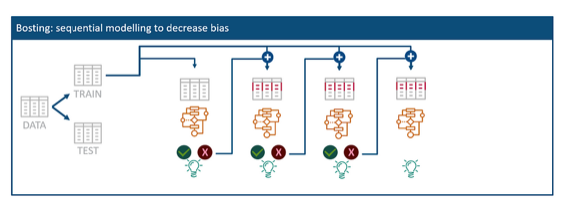
For that, it uses the miss-classified entries of the weak model with some other random data to create a new model. Therefore, the different models are not randomly chosen but are mainly influenced by wrong classified entries of the previous model. The steps for this technique are the following:
- Traininitial(weak)model
Create a subset of the data and train a weak learning model which is assumed to be the final ensemble model at this stage. Analyze the results of the given training data set which should identify those entries that were misclassified. - Update weights and train a new model
ofYou create a new random subset of the original training data but weight those misclassified entries higher. This dataset is then used to train a new model. - Aggregate the new model with the ensemble model
The next model should perform better on the more difficult entries and will be combined (aggregated) with the previous one into the new final ensemble model.
The process can be repeated multiple times and continuously update the ensemble model until the prediction power is good enough.
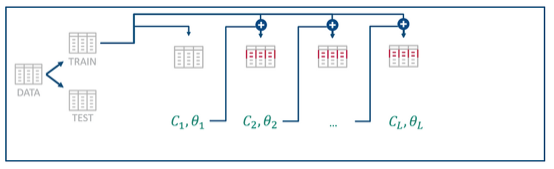
In comparison to Bagging, this technique uses weighted voting or weighted averaging based on the coefficients of the models that are considered together with their predictions. Therefore, this model can reduce underfitting, but might also tend to overfit sometimes.
#4: Conclusion: Differences
Since we learned briefly how bagging and boosting work, I would like to put the focus now on comparing both methods against each other.
Differences
- Data partition| whole data vs. bias
While bagging uses random bags out of the training data for all models independently, boosting puts higher importance on misclassified data of the upcoming models. - Models| independent vs. sequences
Bagging creates independent models that are aggregated together. However, boosting updates the existing model with the new ones in a sequence. - Goal| variance vs. bias
Another difference is the fact that bagging aims to reduce the variance, but boosting tries to reduce the bias. Therefore, bagging can help to decrease overfitting, and boosting can reduce underfitting. - Function| weighted vs. non-weighted
The final function to predict the outcome uses equally weighted average or equally weighted voting aggregations within the bagging technique. Boosting uses weighted majority vote or weighted average functions with more weight to those with better performance on training data.
References
[1]: Bühlmann, Peter. (2012). Bagging, Boosting and Ensemble Methods. Handbook of Computational Statistics. 10.1007/978–3–642–21551–3_33.
[2]: Banerjee, Prashant. Bagging vs Boosting @kaggle: https://www.kaggle.com/prashant111/bagging-vs-boosting



 Follow us on LinkedIn
Follow us on LinkedIn


